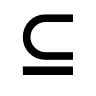| HTML | Meaning | |
|---|---|---|
| ⊂ |
⊂⊂U+2282 |
Subset of The Subset of symbol, denoted as ⊂, is used in set theory to indicate that one set is a subset of another but not equal to it. |
| ⊆ |
⊆⊆U+2286 |
Subset of or Equal to The Subset of or Equal to symbol, denoted as ⊆, indicates that one set is either a subset of another or equal to it. |
| ⊄ |
⊄⊄U+2284 |
Not Subset of The Not Subset of symbol, denoted as ⊄, indicates that one set is not a subset of another, showing non-inclusion. |
| ⊈ |
⊈U+2288 |
Not Subset of or Equal to The Not Subset of or Equal to symbol, denoted as ⊈, signifies that one set is neither a subset of another nor equal to it. |
| ⊃ |
⊃⊃U+2283 |
Superset of The Superset of symbol, denoted as ⊃, is used to indicate that one set is a superset of another but not equal to it. |
| ⊇ |
⊇⊇U+2287 |
Superset of or Equal to The Superset of or Equal to symbol, denoted as ⊇, indicates that one set is either a superset of another or equal to it. |
| ∈ |
∈∈U+2208 |
Element of Indicates that an object is an element of a set. |
What is the "Subset of" Symbol?
The Subset of symbol, represented by ⊂, signifies that one set is contained within another but is not identical to it. For instance, if we have sets A = {1, 2, 3} and B = {1, 2, 3, 4, 5}, it can be expressed as A ⊂ B, indicating that A is a subset of B.
What is the "Subset of or Equal" to Symbol?
The Subset of or Equal to symbol, represented by ⊆, indicates that one set is either contained within another or is identical to it. For the same sets A and B, A ⊆ B is also correct because A is a subset of B. However, if A = {1, 2, 3} and B = {1, 2, 3}, A ⊆ B would be the appropriate notation as the two sets are equal.
How to Differentiate Between the Subset Symbols
It's crucial to understand the difference between the two symbols to avoid confusion. Remember that ⊂ means strict subset (not equal), while ⊆ means subset or equal. The latter symbol allows for the possibility that the two sets being compared might be identical.
Applications and Unique Uses of the Subset Symbols
The subset symbols (⊂ and ⊆) are fundamental in various mathematical and computational contexts:
- Set Theory: Used to express relationships between sets.
- Mathematics: Appears across different fields to depict set relationships.
- Computer Science: Essential in algorithms and data structures for expressing set relationships and operations.
Typing the Subset Symbols
- Windows: For ⊂, use Alt+
8834; for ⊆, use Alt+8838. - Mac: Access both symbols via the Character Viewer.
- Linux: For ⊂, use Ctrl+Shift+u then
2282; for ⊆, follow with2286. - HTML: For ⊂, use
⊂or⊂; for ⊆, use⊆or⊆. - LaTeX: For ⊂, type
\subset; for ⊆, type\subseteq.
Symbols' Images